The Entropy Conundrum
Post-training with Reinforcement Learning and its impact on the entropy of the model
Before we dig deep into what impact post-training a language model with reinforcement learning has on the underlying model parameters, it is important to understand one of the main ideas in machine learning - Entropy.
What is entropy?
In simple words, entropy is a measure of ‘surprise’ from a certain outcome. Suppose we have a heavily biased coin that when flipped yields heads about 99% of the times and yields tails about 1% of the time. If such a coin is flipped and it landed a head, how surprised would you be? Not very, isn’t it? In this context, we could say that the entropy of the underlying probability distribution (H or T) is quite low.
Another way to look at it, would be to say that entropy is the level of ‘choice’ one has when making a certain decision. Say you are looking to rent a flat in your neighbourhood and there are a 1000 different options. Certainly, you will have specific constraints on budget, the size of the place, access to public transport etc. which will narrow down the list of possible choices. Now this could be in the hundreds (higher entropy) or this could be in the tens (lower entropy).
For a more technical treatment to what entropy is and how the Shannon entropy formula came about, refer to the post in Stack Exchange here.
If 𝑋 is a discrete random variable then its entropy is given by the formula.
Scipy provides a method to calculate Shannon entropy and it is worth going through the code here. But here is a more intuitive low-level understanding of how entropy is calculated and how it changes as the underlying distribution changes.
Say D is a discrete random variable with a certain underlying probability distribution. This code block shows how its entropy changes as the distribution changes.
Case 1
D = [0.5, 0.5]
entropy_D = -(0.5 * np.log(0.5) + 0.5 * np.log(0.5))
np.float64(0.6931471805599453)
Case 2
D2 = [0.9, 0.1]
entropy_D2 = -(0.9 * np.log(0.9) + 0.1 * np.log(0.1))
np.float64(0.3250829733914482)
Lower the entropy → Sharper the distribution.
Why is entropy important?
In the context of machine learning, entropy tells us how ‘confident’ a certain model is when making predictions. In classical machine learning world, low entropy was a great thing. We didn’t want models to frequently sit on the fence about classifying text into one of a handful of different sentiments.
In fact, one of the key methods used to improve model performance was a technique called ‘Active Learning’ that involved identifying predictions with high entropy values and curating human labelled inputs to further refine the model. This worked great as the model continued to improve performance on a certain task to match human performance.
Entropy in the context of Language Models
In the context of large language models, entropy defines the certainty with which the model outputs a certain token in a sequence from its entire vocabulary.
The plot below shows entropy at various tokens when the Qwen-2.5-7B model is asked to write a joke. Notice how there is really just 2 spikes in the graph. Entropy is at near 0 levels throughout otherwise - The model knows the joke quite well and there is no uncertainty involved on what to say next at the end of each token in the sequence. A low entropy is preferred!
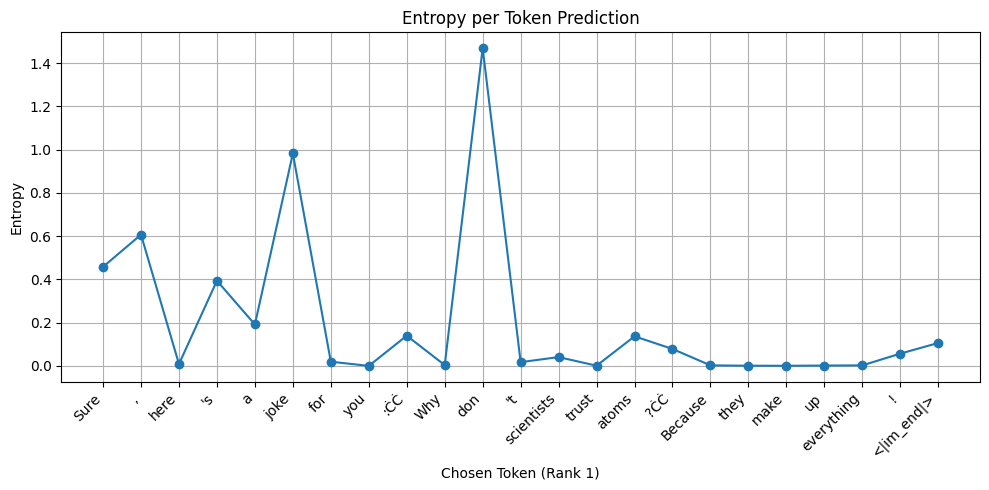
Now here is another one. Here the model is asked to write a poem. See the difference?
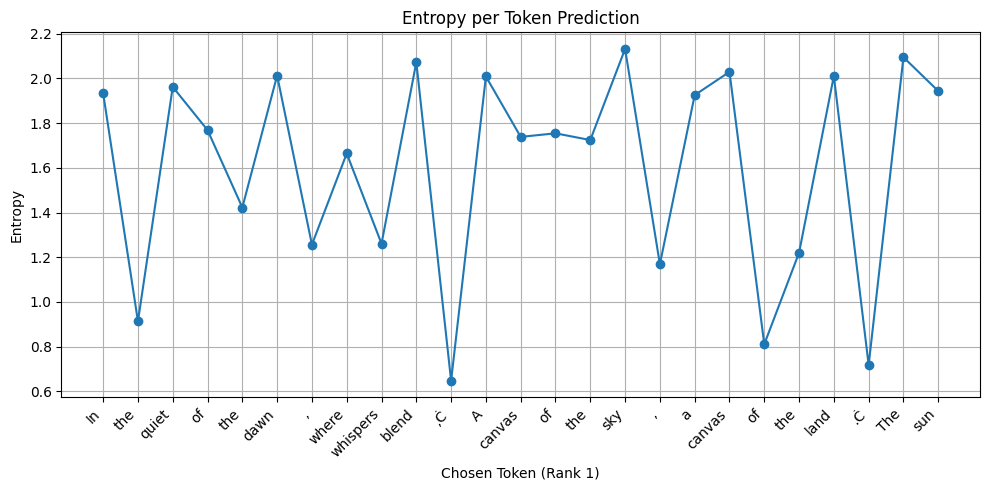
Writing a poem is inherently a creative endeavour and the model has to deliberate quite significantly on the choice of its ‘tokens’. A higher entropy is preferred!
What happens to entropy when a model is post-trained with reinforcement learning?
Now on to the main topic, what happens to entropy when the model is pre-trained and then post-trained with reinforcement learning? Here are two charts from the GPT-4 release that explains this.
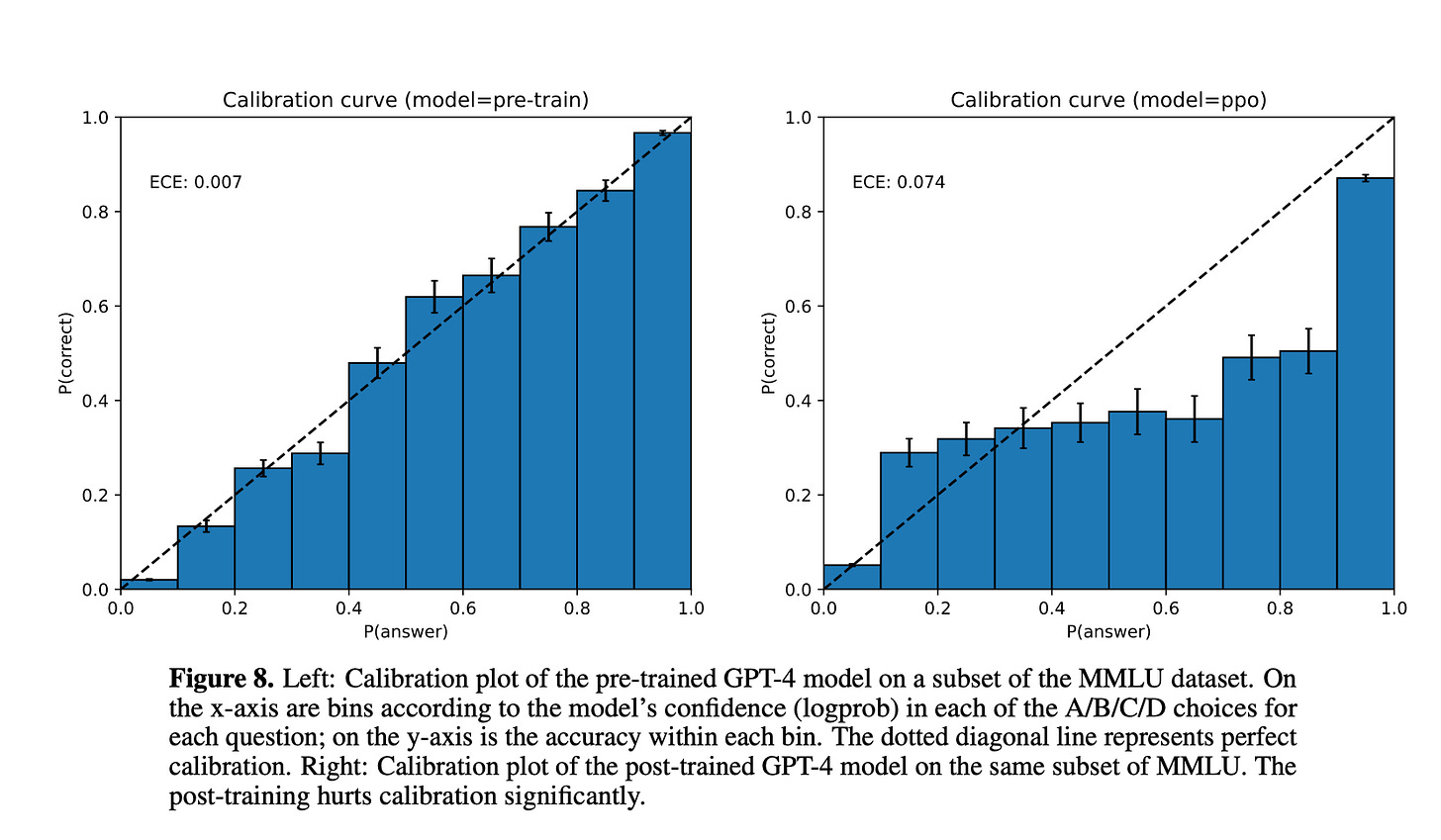
The main takeaway from the chart is this - The pre-trained model’s log probabilities across the 4 choices (A/B/C/D) exhibit near perfect correlation with the actual answer correctness on the MMLU benchmark. This calibration is lost post-PPO. The model is much more confident (as measured by its logprobs on the response), whether or not its response is actually correct.
Entropy collapse is one of the biggest issues with reinforcement tuning language models. This often leads to a loss of exploration, a complete lack of creativity in model output and an inability to generalise beyond the domain the model is tuned for. For general purpose language or reasoning models, this often is undesirable.
Here is another example from the Skywork open reasoner series. Their report on this subject is a pretty interesting deep dive. The chart on the right shows entropy collapse, inspite of adding an entropy regulaiser, as training progresses in a PPO style RFT loop.
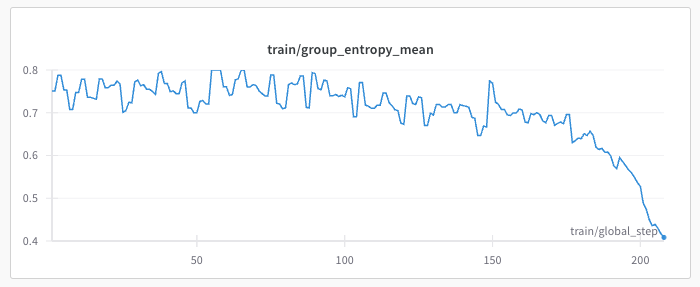
Here are some charts from my own experiments last week with reinforcement fine-tuning the Qwen2.5-7B model on a Wordle environemnt (more on this later).
Result 1: The first chart shows the rapid and steep decline in mean entropy across generations from a single group as training progresses.
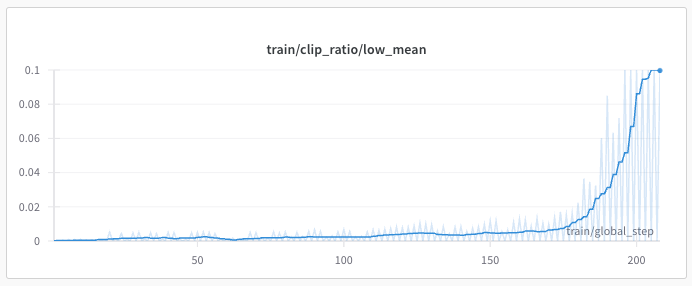
Result 2: And this second chart shows the loss function aggressively clipping the parameter updates as the model pushes the log probabilities of the tokens below the lower end of the trust region.
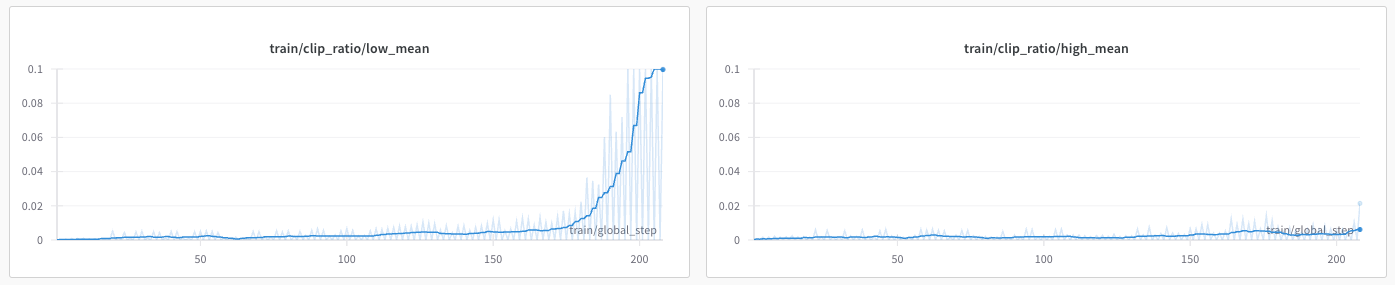
Result 3: This chart below shows a side by side comparison of the mean low-clip and high-clip ratios. The model is trying to push a handful tokens above the upper end of the trust region (right), but an enormous amount of tokens below the lower-clip (left).
In other words, the RFT loop forces the model to learn this new distribution of producing tokens that have a high correlation to the rewards.
This is both good and bad.
This is good because if the reward signals are designed carefully, then it is possible to get the model to learn an optimal policy for a very specific domain and perform exceptionally well here.
This is bad because of a whole host of things - the biggest of which is that training becomes super brittle. The loss of generality, heterogeneity in output, the inability to control creativity using temperature are some of the others.
And the solution?
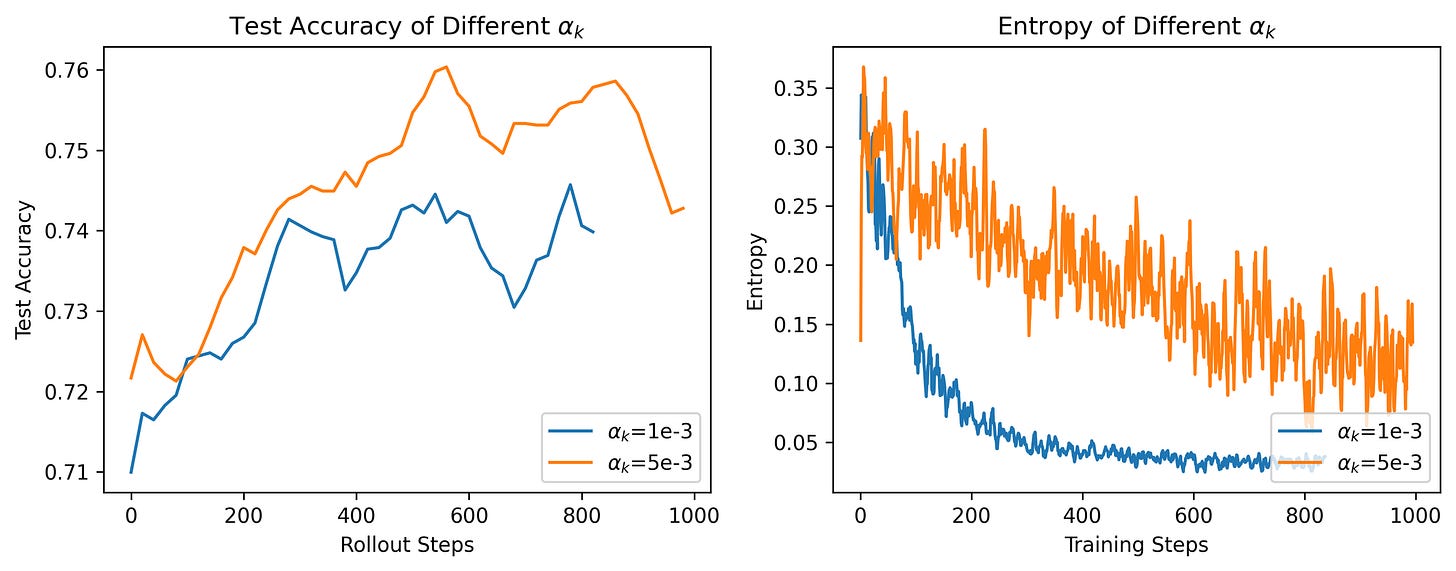
One way to solve this problem is to add an entropy regulariser to the loss term as the team at Skywork AI have done.
Their formulation of the modified GRPO loss function involves getting rid of the KL divergence penalty and replacing that with this entropy regulariser term. Interestingly, their findings note that training stability depends on both the data and the regulariser co-efficient (read as, training is brittle). Their response is to set a target entropy and adaptively modify the alpha value. Will this work? It did for them. But as with all other things in RL, hard to say if this will generalise.
Another way to solve this problem, is to clip the advantage values in the loss function to a narrow region, say (-1 to +1). My own experience has been that just a handful of groups/batches with large reward standard deviations can completely derail the training loop in RL. The only signal/feed we provide are the advantage values. And they can sometimes blow-up training.
The below example shows how in a group of 24 generations, if only 1 is given a positive reward, the update step can push the log probabilities of the tokens in that generation quite significantly.
import numpy as np
l = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1]
m = np.mean(l)
s = np.std(l)
adv =[a-m for a in l]/s
array([-0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, -0.20851441, 4.79583152])
Wrap-up
Post-training is an absolutely fascinating area of study. This post shows one of many many unsolved open challenges the field faces.